A rational number can be written in the form of q p , q n = 0 so there lie an infinite rational numbers between 2 and 3 we know, 2 = 1 4 1 4 and 3 = 1 7 3 2 Hence,Click here👆to get an answer to your question ️ Add 7√(2) 5√(3) and √(2) 7√(3)Resolvemos problemas de matemáticas respondiendo a preguntas sobre tus deberes de álgebra, geometría, trigonometría, cálculo diferencial y estadísticas con explicaciones paso a paso, como un tutor de matemáticas

Why Do We Rationalize The Denominator By Brett Berry Math Hacks Medium
Add 22 37 19 25 37 51 82
Add 22 37 19 25 37 51 82-Distance in a 3D coordinate space The distance between two points on a 3D coordinate plane can be found using the following distance formula d = √ (x2 x1)2 (y2 y1)2 (z2 z1)2 where (x 1, y 1, z 1) and (x 2, y 2, z 2) are the 3D coordinates of the two points involved Like the 2D version of the formula, it does not matter which of4/8/18 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers by




Adding And Subtracting With Integers Integers Siyavula
1/6/21 Question 7 If √3 = 1732 and √2 = 1414, find the value of 1 √ 3 − √ 2 (a) 0318 (b) 3146 (c) 1 3146 (d) 1732 − − − − √ – 1414 − − − − √ Answer Answer (b) 3146Here A = 2 , m= 1 and n= 1/2 ;15/4/ Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries Students (upto class 102) preparing for All Government Exams, CBSE Board Exam, ICSE Board Exam, State Board Exam, JEE (MainsAdvance) and NEET can ask questions from any subject and get quick answers by
(i) (√(3) √(7))^2 =(√(3))^2 (√(7))^2 2 ×√(3)×√(7) {∵ (ab)^2 = a^2 b^2 2ab } = 3 7 2 √(21) = 10 2 √(21) (ii) (√(5) √(3))^2Download the Free PDF of RD Sharma Class 9 Solutions Chapter 1 MCQs from this blog To now more, you can read the whole blogTopicसिद्ध कीजिए कि रूट 2,3,5,7,11 एक अपरिमेय संख्या है class 10th vvi question, important question for examination, 2 marks
2√2𝑖2 = 14𝑖 2√2(−1) = −7𝑖 √2 × √2 √2 = −7√2𝑖 2 Overall Hint Multiply the terms in the numerator then subtract the terms of denominator then change the terms i^2 to –1 and rationalise the denominator of the obtained product to give the expression in the form aib Exercise 52 1 Find the modulus and the argument13/8/18 (i) (√5 √2) 2 We need to apply the formula (a b) 2 = a 2 2ab b 2 to find value of (√5 √2) 2 (√5 √2) 2 = (√5) 2 2 x √5 x √2 (√2) 2 = 5 2√10 2 = 7 2√10 Therefore, on simplifying (√5 √2) 2, we get 72√0 (ii) (√5 √2) (√5 √2)11/9/ Add (3√27√3) and (√2−5√3) Divide 5√11 by 3√33 Multiply 2√15 by 7√5 Simplify (√5√7)^2 Simplify (√4−√13)(√4√13) Simplify (9−√3)(9√3) Simplify (3√5−5√2)(4√53√2) Rationalise the denominator of 8




Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 V




How To Find The Product And Sum Of Two Or More Numbers Owlcation
11/7/18 Transcript Example 13 Add 2 √2 5 √3 and √2 3 √3 Here, both numbers have root in it So, we combine the numbers with the same root Combining 2 √2 & √2 and 5√3 & 3 √3, and then solving 2 √2 5 √3 √2 – 3 √3 = (2 √2 √2) (5√3 – 3 √3) = √2 (2 1) √3(5 –Write in Ascending Order 6√5, 7√3 and 8√2 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6 Question Bank Solutions 145 Concept Notes & Videos 431 Syllabus Advertisement Remove all ads Write in Ascending OrderShare It On Facebook Twitter Email 1 Answer 0 votes answered by AbhishekAnand (871k points) selected Aug 17




3 Number What Is There To Know Adding It Up Helping Children Learn Mathematics The National Academies Press




Multiplying And Dividing Radical Expressions
8/9/21 RD Sharma Class 9 Solutions Chapter 1 MCQS Class 9 Maths exams are made easier All thanks to the RD Sharma Solutions Class 9 MathsBe it your exams or class assignments, we have got your back! √100以上 add (2√2 √3) and 7√2 Add 2/213/7 SolutionIfx is the regular price of one basket,then3x 14=0,so3x =186,andx =$62 9If!4√3 Question 4 4√5 Question 5 30 Question 6 53√3 √ Question 7 31−9√2 Question 8 −512√18 Question 9 3 Question 10 8√3 Question 11 313/5/21 Next Simplify (√4−√13) (√4√13)→ Chapter 1 Class 9 Number Systems (Term 1) Concept wise Rationalising Rationalising denominator of irrational number Add (3√27√3) and (√2−5√3) Divide 5√11 by 3√33 Multiply 2√15 by 7√5 Simplify (√5√7)^2 You are here Simplify (√4−√13) (√4√13) Simplify (9−√3) (9



What Is 2 7 3 7




2 9 Square Roots And Cube Roots Notes
(i) 3 √ 2 − 2 √ 3 3 √ 2 2 √ 3 √ 12 √ 3 − √ 2 (ii) 7 3 √ 5 3 √ 5 − 7 − 3 √ 5 3 − √ 5 Mathematics RS Aggarwal (, 21) All19/6/21 Obtained all other zeroes of the polynomial 4x^4 x^3 72x^2 18x, if two of its zeroes are 3√2 and 3√2 asked in Mathematics by AnjaliVarma ( 294k points) polynomials6/7/21 ∴ √2 is the simplest form of the rationalising factor of √32 Now, 5√2 x √2 = 5 x 2 = 10, which is a rational number ∴ √2 is the simplest form of the rationalising factor of √50 Now, 3√3 x √3 = 3 x 3 = 9, which is a rational number ∴ √ 3 is the



Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 Studyrankersonline




Simplify 4 5 6 2 3 8 3 7 12
If They Are AP Find the Common Difference 3, 3 √ 2 , 3 2 √ 2 , 3 3 √ 2 Maharashtra State Board SSC (English Medium) 10th Standard Board Exam Question Papers 238 Textbook Solutions MCQ Online Tests 39 Important Solutions 2786 Question Bank Solutions 9112Solution = 5√3 18√3 − 2√3 In the given expression, the radical terms are having same index So, we have easily combine them by factoring √3 = (5 18 2) √ 3 = 21 √ 3 (ii) 43√5 23√513/5/21 Rationalising denominator of irrational number Add (3√27√3) and (√2−5√3) You are here Divide 5√11 by 3√33




Ex 7 6 1 Solve 2 3 1 7 Teachoo Class 6




Adding And Subtracting Radical Expressions
Expand and simplify with single brackets Expand the brackets to give the following expression Eg 2 (x 5) 3 (x − 1) = 2x 10 3x − 3) = 5x 7 Remember expressions with two terms like 5x 7 are known as binomials 2 Expand and simplify with two or more bracketsThus, (3 √23) √23 is a rational number iii) 2√7 / 7√7 2√7 ÷ 7√7 = 2/7, which is in the form of p/q and hence a rational number Thus, 2√7 / 7√7 is a rational number iv) 1/√2 1/√2 = (1/√2) × (√2/√2) = √2/2 = 1414/21 (x 2√2)(x √5) = x² (2√2 √5)x 2√10 = x² 2x√2 x√5 2√10 2 (x² 2x√2 x√5 2√10)(x 3) = x³ 2√2x² √5x² 2√10x 3x² 6√2x 3√5x 6√10 = x³ 3x² 2x²√2 x²√5 6x√2 3x√5 2x√10 6√10 This is not matching any options so we add two more zero's




Square Root Of 504 How To Find Square Root Of 504 Solved




Solve Solve Linear And Quadratic Equations With Step By Step Math Problem Solver
I) 1/√7 ii) 1/(√7 √6) iii) 1/(√5 √2) iv) 1/(√7 2) Solution Rationalization is the process of eliminating a radical or an imaginary number from the denominator of an algebraic fraction i) 1/√7 Dividing and multiplying by √7, we getThe roots to these are not whole numbers or fractions, and so they have irrational values They are usually written as decimals to a given approximation For example √ 2 = 1414 to 3 decimal places, √ 3 = 1732 to 3 decimal places When we have square roots which give irrational numbers we call them surds So √ 2 and √ 3Now we know that 2^1 = 2 and 2^(1/2) = Root



Problem Solving If 3 2 7 5 4 23 7 6 47 And 9 8 79 To What Is 10 9 Equal Quora



If 6 9 61 5 8 46 4 7 33 And 3 6 22 Then What Does 1 4 Quora
17/8/18 If z 1 = √3 i √3 and z 2 = √3 i , then find the quadrant in which (z 1 /z 2) lies complex numbers and quadratic equation;Rationalising denominator of irrational number Add (3√27√3) and (√2−5√3) Divide 5√11 by 3√33Weekly Subscription $249 USD por semana hasta cancelar Suscripción mensual $799 USD por cada mes hasta cancelar Suscripción anual $3499 USD por cada año hasta cancelar




How To Add And Subtract Square Roots 9 Steps With Pictures




Simplify 3 5 5 2 4 5 3 2 With Video Teachoo Rationalising
Answer (1 of 9) The problem, (√2√3)^2 =(√2)^2(√3)^22(√2*√3) =232√6 =52√6 Now, 2√6=√24=(approx) So, (√2√3)^2 =52√6 =54Answer (3) 3√3 It is an example of adding two irrational numbers 2√3 √3 We can see that there are two terms that contain two √3, one with coefficient 2 and the other with coefficient 1, and there would be 2 1 = 31/7/21 To add and subtract square roots, you need to combine square roots with the same radical term This means that you add or subtract 2√3 and 4√3, but not 2√3 and 2√5 There are many cases where you can actually simplify the number inside the
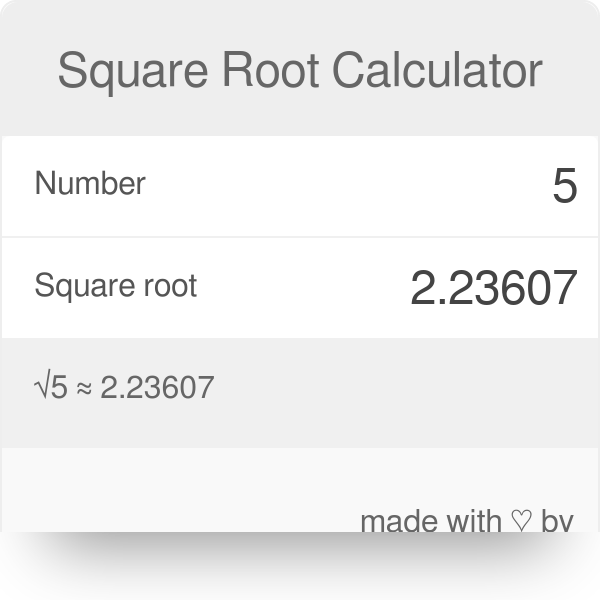



Square Root Calculator Find The Square Root In One Easy Step




Add 2 4 5 And 3 5 6 Youtube
Rationalise the Denominators of 2√5 3√2/2√5 3√2 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6 Question Bank Solutions 145 Concept Notes & Videos 431 Syllabus Advertisement Remove all ads Rationalise theTherefore we can write 2^(11/2) as 2^1 * 2^(1/2) ;Answer (1 of 19) Let's simplify 2\sqrt{3}\sqrt{3} = \sqrt{4} \times \sqrt{3} \sqrt{3} \sqrt{4 \times 3} \sqrt{3} \sqrt{12} \sqrt{3} That's as simple as it gets without trying to represent it in a decimal representation, if you want the value you can go to a calculator and you would



What Is 2 3 3 9




Expert Verified 5 2 3 7 4 3 A B 3 Find The Value Of A And B Of The Following Brainly In
Description The sum of a positive number and its reciprocal is twice the difference of the number and its reciprocal The number is (A) √2 (B) 1/√2 √3Surds are the square roots (√) of numbers that cannot be simplified into a whole or rational number It cannot be accurately represented in a fraction In other words, a surd is a root of the whole number that has an irrational value Consider an example, √2 ≈ It is more accurate if we leave it as a surd √2If x > 0, then ( √ 4 x √ 9 x) 2 = 5 x 6 x 13 x 25 x 30 x So, you were trying to be a good test taker and practice for the GRE with PowerPrep online Buuuut then you had some questions about the quant section—specifically question 17 of the second Quantitative section of Practice Test 1 Those questions testing our knowledge of




Celebrating The Playful Magic Of John Horton Conway Quanta Magazine




Chapter 7 Radicals Radical Functions And Rational Exponents Ppt Video Online Download
√ 2 or √ 3?Answer (1 of ) This is the basic method to calculate the value of 2^(3/2) First of all rearrange the term ie 2^(11/2) Using the formula A^(mn) = A^m * A^n ;3 Proof This follows from the squeeze theorem, the estimate 1 ≤ n p n √ n ≤ n √ 2n = n √ 2n √ n, and lim n→∞ n 2 = lim n→∞ n = 1 2213(a) Suppose that {a




Multiply 3 Root 5 By 2 Root 6 Root 15 By 4 Root 5 2 Root 6 By 3 Root 3 3 Root 8 By 3 Root 2 Youtube



What Is The Sum Of 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 95 97 99 Quora
11/6/18 3√2 7√3 √2 5√3 4√2 2√3 kattyahto8 and 5 more users found this answer helpful heart outlined Thanks 3 star star star starWrite in Ascending Order 6√5, 7√3, and 8√2 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6 Question Bank Solutions 145 Concept Notes & Videos 431 Syllabus Advertisement Remove all ads Write in Ascending 解:对于函数g(x)有: π/2 √3(6k1)π/3≤x≤π/2√3(6k1)π/3, x≥π/2√3(6k1)π/3或者 x≤π/2 √3(6k1)π/3, x≥π/2



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




Addition Adding 3 Numbers Free Printable Worksheets Worksheetfun
The correct option is A 66 The value can be found by substituting the given values in 2(√(3)√(2))/√(3) √(2) = 2(1714)/17 14 = 62/03 = 66CAP´ITULO 10 SOLUCIONES 102 DESARROLLADAS Si r > 1, claramente l´ıma n = ∞ (n´otese que 1 1 n n → e) y por tanto S no converge Finalmente, para r = 1, S converge por el criterio de Leibniz, ya que en este caso l´ımaClick here👆to get an answer to your question ️ Add (2√(2) 5√(3) 7√(5)) and (3√(3) √(2) √(5))



2 3 2 3




Answered 7 10 Function Notation Express The Bartleby
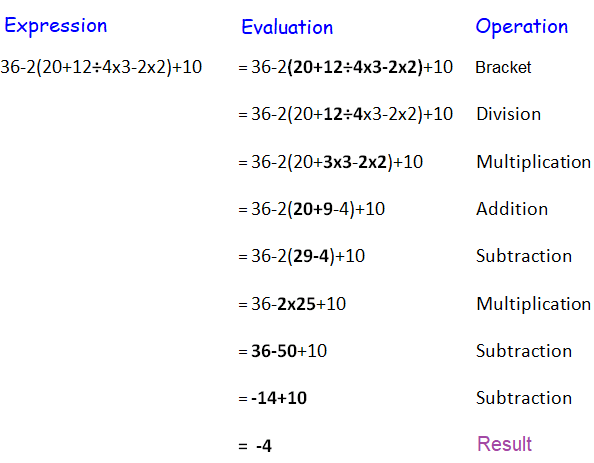



Bodmas Rule




Addition Of Unlike Fractions Adding Fractions With Different Denomin




True Or False Nz Maths
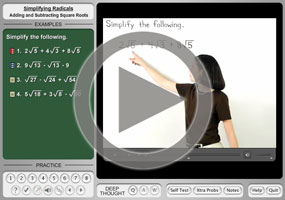



Adding Subtracting Radicals Square Roots Purplemath




Solved 5 12 Describe Verbally The Inverse Of The State Exercises Then Express Both The Given Statement And Its Inverse Ment Symbolically Add 2 To X 6 Multiply X By 5 5 7 Subtract



How To Sum 1 1 2 3 1 2 3 4 1 3 4 5 For Up To 10 Terms Quora



Vectors




Adding And Subtracting Negative Numbers Worksheets




Confidential 1 Algebra1 Adding And Subtracting Radical Expressions Ppt Download




Find The Sum Of The Series 1 3 2 5 4 7 8 9 16 Oo Youtube




Numbers In Python Real Python




How Long Has The Order Of Priority Of Arithmetical Operations Been Widely Taught In High Schools History Of Science And Mathematics Stack Exchange




How To Add And Subtract Square Roots 9 Steps With Pictures




How To Find 1 2 1 4 1 8 Video Lesson Transcript Study Com




The Symbol Means Radical Or Square Root A X2 2x



If 2 3 8 3 7 27 4 5 32 5 8 60 6 7 72 Then The Value Of 7 8 Is Quora




Lcm Of 2 3 And 7 How To Find Lcm Of 2 3 7




Add 3 2 7 3 And 2 5 3 Brainly In




Adding And Subtracting Polynomials Video Lessons Examples Solutions



Surds Mathematics Gcse Revision




Add 3 2 7 3 And 2 5 3 Brainly In




What Are Natural Numbers Definition Examples And Facts




Accgeounit 2 Methods For Solving Quadratic Equations




Add 2 3 5 5 7 7 And 3 5 3 7 Brainly In




Classroom Lessons Math Solutions




If 5 2 3 7 4 3 A B 3 Then The Value Of A And B



3




Rd Sharma Solutions For Class 8 Chapter 1 Rational Numbers Download Free Pdf




Add 3 2 7 3 And 2 5 3 Rational Numbers Video Teachoo



1




Solved Ises 5 12 Describe Verbally The Inverse Of The State Chegg Com




Adding And Subtracting With Integers Integers Siyavula




Simplify 7 3 10 3 2 5 6 5 3 2 15 3 2 V




Solved 1 Express The Following Rule In Function Notation Chegg Com




Perfect Number Wikipedia




Math Tricks Explained The New York Times




How To Solve Surds 2 Four Essential Surd Techniques Suresolv



What Is 6 9 2 3
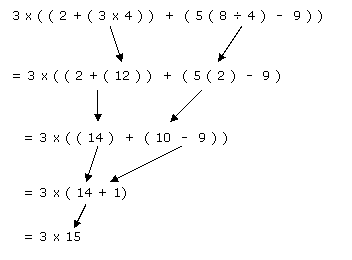



Order Of Operations




Simplifying Square Root Expressions No Variables Video Khan Academy




Wolfram Alpha Examples Step By Step Solutions
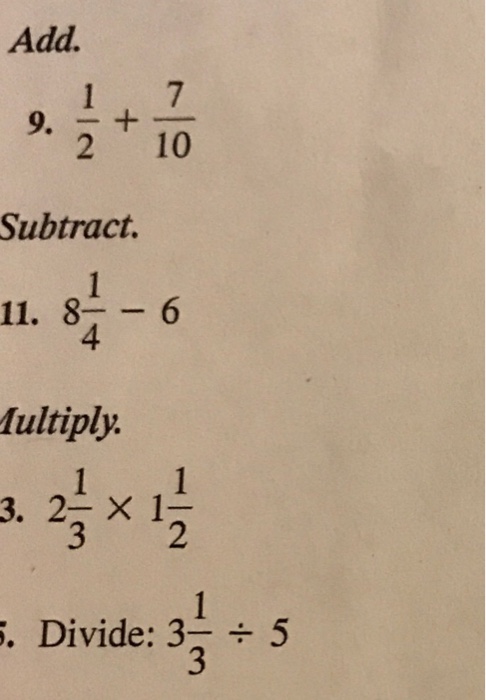



Solved Add 1 2 7 10 Subtract 8 1 4 6 Multiply 2 Chegg Com




How To Add And Subtract Square Roots 9 Steps With Pictures



1




Find The Values Of A And B If 7 3 5 3 5 7 3 5 3 5




Rd Sharma Solutions Class 9 Maths Chapter 3 Rationalisation Updated For 21 22



Danville Edu



Rationalize The Denominator And Simplify I 3 2 3 2 Ii 5 2 3 7 4 3 Sarthaks Econnect Largest Online Education Community




Solved Skills 7 10 Function Notation Express The Rule In Chegg Com




How To Add And Subtract Square Roots 9 Steps With Pictures




Solved Skills 7 10 Function Notation Express The Rule In Chegg Com




Rationalise The Denominator 4 2 Under Square Root 3 Under Square Root 7 Plz Explain To Me Step By Brainly In




Simplify Add Or Subtract Fractions With Step By Step Math Problem Solver




How To Find The General Term Of Sequences Owlcation




Why Do We Rationalize The Denominator By Brett Berry Math Hacks Medium




Add 2 5 5 7 3 10 1 5 Mathematics Topperlearning Com Ewwxcpjj




The Arithmetic Mean Between A And B Is Twice The Geometric Mean Between A And B Prove That A B 7 4 3 Or 7 4 3 Mathematics Topperlearning Com 3dl3jill




Simplifying Square Root Expressions No Variables Video Khan Academy




Complex Numbers




Adding Square Roots Study Com



Solve Equations With Square Roots Elementary Algebra
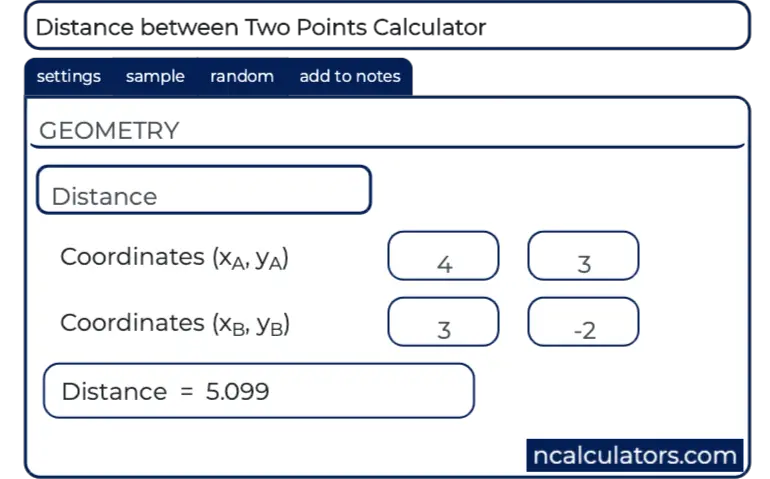



Distance Between Two Points Calculator




Sum Of N Squares Part 2 Video Khan Academy



Square Root Of 2 Wikipedia



Solve Quadratic Equations Using The Quadratic Formula Elementary Algebra




Add 2 Root 2 5 Root 3 And Root 2 3 Root 3 Youtube



Python Challenges 1 Exercises Practice Solution W3resource




How To Add And Subtract Square Roots 9 Steps With Pictures




Adding And Subtracting With Integers Integers Siyavula




3 9 Adding And Subtracting Mixed Numbers Do Now Add Or Subtract Ppt Video Online Download




Solved To Calculate The Standard Deviation Of Those Numbers Chegg Com



Web Auburn Edu




Simplifying Radical Expressions
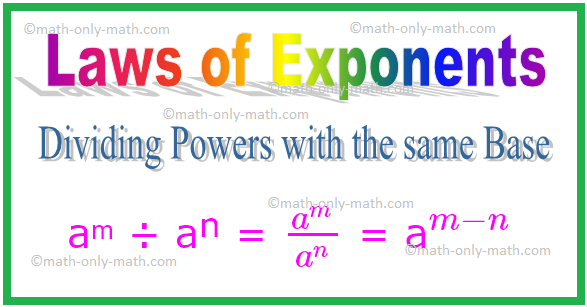



Laws Of Exponents Exponent Rules Exponent Laws Definition Examples




Prove That The Following Are Irrational I 1 2 Ii 7 5 Iii 6 2




Add 2 3 5 2 And 3 2 2 2 2 5 3 7 5 And 3 3 2 5 2 3 7 1 2 2 6 11 Youtube



0 件のコメント:
コメントを投稿